Vertex of parabola is y=
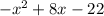 at (4,6)
at (4,6)
Explanation:
The given equation of parabola is y=
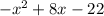
Simplifying the equation,
y=
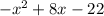
y=
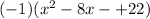
y=
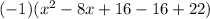
y=
![(-1)[(x^(2) -8x + 16)-(16-22)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/gxmdnt6i3n3si8e9aljq13b0v5dyp1ve31.png)
y=
![(-1)[(x-4)^(2)+(+6)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/vzsck79hsrbruv4h56n1jy2q0a9oocu8ng.png)
y=
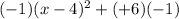
y=
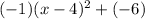
The general equation of parabola is y = y=
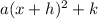
Where, (h,k) is vertex of parabola.
On comparing the equations
we get,
Vertex of parabola is y=
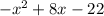 at (4,-6)
at (4,-6)