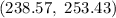Question

A laboratory tested 12 chicken eggs and found that the mean cholesterol was 246 mg with a standard deviation of 11.7 mg. Construct a 95% CI for the true mean cholesterol content of all such eggs.

Answer 1

Answer:
`(238.57,\ 253.43)`

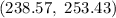
Explanation:

When population standard deviation is not given , then the formula to find the confidence interval for population mean is given by :-

`\overline{x}\pm t_(\alpha/2)(s)/(√(n))`

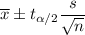
, where
`\overline{x}` = sample mean.

s= sample standard deviation.

n= sample size.

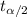`t_(\alpha/2)` = Critical t-value (two tailed ).

Given : n= 12 ,
`\overline{x}=246` , s=11.7

Significance level =
`\alpha=1-0.95=0.05`

Degree of freedom : n- 1= 11

Using t- distribution , the critical t-value =
`t_(\alpha/2, df)=t_(0.025,\ 11)=2.2010`

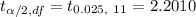
Now, the required 95% CI for the true mean cholesterol content of all such eggs will be :-

`246\pm (2.2010)(11.7)/(√(12))\\\\=246\pm(2.2010)(3.3775)\\\\=\\\\=246\pm7.4339=(246-7.4338,\ 246+ 7.4338)\\\\=(238.5662,\ 253.4338)\approx(238.57,\ 253.43)`

Hence, the required confidence interval =
`(238.57,\ 253.43)`