Question

The production demand for widgets for a​ 250-workday year is​7,500 units. Ordering costs are​ $25.00 per order and carrying costs are​ $9.00 per unit per year. Four days must be allowed between order placement and order receipt.What is the number of orders per​ year, assuming known and constant​ variables?A.107B.27C.37D.127The answer is C but can anyone explain why?

Answer 1

C 37 units

Step-by-step explanation:

First, we solve for the Economic order quantity given the annual demand and inventory cost:

`Q_(opt) = \sqrt{(2DS)/(H)}`

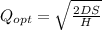
Where:

D = annual demand= 7,500

S= setup cost = ordering cost= 25

H= Holding Cost= 9.00

`Q_(opt) = \sqrt{(2(7,500)(25))/(9)}`

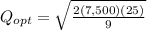
EOQ = 204.1241452

Now, each order will be of 204 units considering the demand is for 7,500 units we will divide to get the order per year:

7500 / 204 = 36.76 = 37