Answer:
2139 Million years
Step-by-step explanation:
Half life of a material is the time required for the material to decay into half of initial amount.
initially there is 26 grams of uranium-235, and the final amount is 3.25 gram
ratio between initial and final amount =
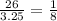
now it is clear that the material have halved 3 times from initial condition
number of half lives passed = 3
number of half lives passed can also be found using the equation
no of half lives =
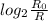
where
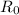 is the initial amount of material and R is the final amount
is the initial amount of material and R is the final amount
∵ Number of half lives =
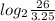
= 3
So, age of rock = half-life X number of half-lives passed
=713000000 X 3
= 2139000000
=2139 Million Years