Question

Two astronauts (each with mass 100 kg) are drifting together through space. They are connected to each other by a rope 5 m in length, and are moving in circles about a point halfway between them (i.e. their center of mass). Each astronaut has a speed of 2 m/s. They then pull on the rope, shortening the distance between them to 1 m. You can simplify the system by treating the astronauts as particles, and assuming the rope has negligible mass. Then solve the following; set up steps 3-7 separately for each part (you can use the same picture for all parts). a. What are the initial angular momentum and rotational energy of the system? b. What are the final angular momentum and rotational energy of the system? (hint: what is the new velocity of each astronaut?). C. How much work was done by the astronauts in shortening the rope?

Answer 1

1000 kgm²/s, 400 J

1000 kgm²/s, 1000 J

600 J

Step-by-step explanation:

m = Mass of astronauts = 100 kg

d = Diameter

r = Radius =
`(d)/(2)`

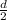
v = Velocity of astronauts = 2 m/s

Angular momentum of the system is given by

`L=mvr+mvr\\\Rightarrow L=2mvr\\\Rightarrow L=2* 100* 2* 2.5\\\Rightarrow L=1000\ kgm^2/s`

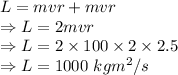
The angular momentum of the system is 1000 kgm²/s

Rotational energy is given by

`K=I\omega^2\\\Rightarrow K=(1)/(2)(mr^2)\left((v)/(r)\right)^2\\\Rightarrow K=mv^2\\\Rightarrow K=100* 2^2\\\Rightarrow K=400\ J`

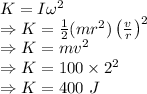
The rotational energy of the system is 400 J

There no external toque present so the initial and final angular momentum will be equal to the initial angular momentum 1000 kgm²/s

`L_i=L_f\\\Rightarrow 2mv_ir_i=2mv_fr_f\\\Rightarrow v_f=(v_ir_i)/(r_f)\\\Rightarrow v_f=(2* 2.5)/(0.5)\\\Rightarrow v_f=10\ m/s`

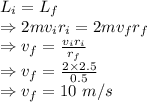
Energy

`E_2=mv_f^2\\\Rightarrow E_2=100* 10\\\Rightarrow E_2=1000\ J`

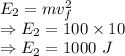
The new energy will be 1000 J

Work done will be the change in the kinetic energy

`W=E_2-E\\\Rightarrow W=1000-400\\\Rightarrow W=600\ J`

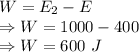
The work done is 600 J