Answer:
The correct option is a) 6.4 m
Explanation:
Let A represents the position of first player B represents the position of second player and C represents the position of the Coach,
According to the question,
AB = 10 meters,
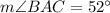
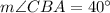
Since, the sum of all interior angles of a triangle is 180°,
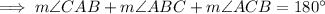
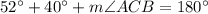
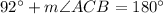
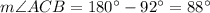
Using law of sine,
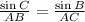
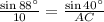
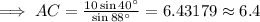
Hence, player 1 is 6.4 meters far from the coach.