Question

A study was conducted to determine if there was a difference in the driving ability of students from West University and East University by sending a survey to a sample of 100 students at both universities. Of the 100 sampled from West University, 15 reported they were involved in a car accident within the past year. Of the 100 randomly sampled students from East University, 12 students reported they were involved in a car accident within the past year.

Answer 1

There is no significant evidence which shows that there is a difference in the driving ability of students from West University and East University, assuming a significance level 0.1

Explanation:

Let p1 be the proportion of West University students who involved in a car accident within the past year

Let p2 be the proportion of East University students who involved in a car accident within the past year

Then

`H_(0):`p1=p2

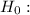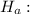`H_(a):`p1≠p2

The formula for the test statistic is given as:

z=
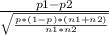`\frac{p1-p2}{\sqrt{(p*(1-p)*(n1+n2))/(n1*n2) } }` where

• p1 is the sample proportion of West University students who involved in a car accident within the past year (0.15)
• p2 is the sample proportion of East University students who involved in a car accident within the past year (0.12)

• p is the pool proportion of p1 and p2 (
  `(15+12)/(100+100)=0.135`)
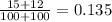• n1 is the sample size of the students from West University (100)
• n2 is the sample size ofthe students from East University (100)

Then we have z=
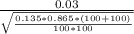`\frac{0.03}{\sqrt{(0.135*0.865*(100+100))/(100*100) } }` ≈ 0.6208

Since this is a two tailed test, corresponding p-value for the test statistic is ≈ 0.5347.

Assuming significance level 0.1, The result is not significant since 0.5347>0.1. Therefore we fail to reject the null hypothesis at 0.1 significance