Question

In a study comparing banks in Germany and Great Britain, a sample of 145 matched pairs of banks was formed. Each pair contained one bank from Germany and one from Great Britain. The pairings were made in such a way that the two members were as similar as possible in regards for factors like size and age. The ratio of total loans outstanding to total assets was calculated for each bank. For this ration, the sample mean difference (German – Great Britain) was 0.0518 and the sample standard deviation of the differences was 0.3055. Test, against a two sided alternative, the null hypothesis that the two population means are equal.

Answer 1

The difference between the two population is mean

Step-by-step explanation:

Let the population mean for Germany and Great Britain be represented by
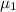`\mu_1` and
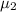`\mu_2` respectively hence

Null hypothesis

`H_o: \mu_1-\mu_2=0`

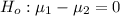
Alternative hypothesis

`H_1: \mu_1-\mu_2\\eq 0`

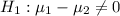
Taking
`\alpha=0.05`

`s_d=0.3055`

`\bar d=\bar x-\bar y=0.0518`

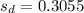
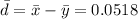
Sample size, n=145

Student’s t statistics is given by

`t=\frac {\bar d \sqrt n}{s_d}=\frac {0.0518* \sqrt 145}{0.3055}=2.042`

From t table,
`t_(n-1,\alpha/2)=t_(144,0.025)=1.977`

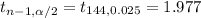
The decision rule is to reject null hypothesis if

`\frac {\bar d \sqrt n}{s_d}>t_(n-1, \alpha/2)`

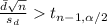
Therefore, we reject the null hypothesis because the computed t value is more than critical value. We conclude that the difference between the two population is mean.