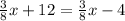Question:
Bradley wrote the beginning of an equation,
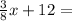
Finish the equation so that the equation will have no solution. Explain how you know.
Answer:
Explanation:
Given
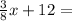
Required
Complete the equation to have no solution
The given equation is a linear equation in form of

Where
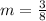
Compare both equations
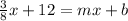
Substitute
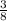 for m
for m
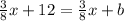
Collect Like Terms

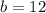
This implies that, for the equation to have a solution the value of b must be 12.
However, for the equation not to have a solution, the value of b must not equal 12
i.e.
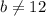
This implies that, we can assume any value, other than 12 for b so that the equation will not have a solution.
Say for instance: b = -4
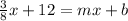
Substitute -4 for b and 3/8x for m. This gives: