Question

A surveyor is conducting measures to see how wide a road is

between points A and B. Using her surveying instrument, she
creates two similar right triangles, AABC - AEDC.
CD = 24 feet, DE=18 feet, BC=60 feet. What is the distance
between A and B?
OA) 24 ft.
OC) 36 ft.
OB) 30 ft.
OD) 45 ft.

Answer 1

D) 45 ft

Explanation:

The two triangles are shown below.

Given:

BC = 60 ft, CD = 24 ft and DE = 18 ft.

Since, the two triangles are similar, their corresponding sides are in proportion.

So,
`(AB)/(DE)=(BC)/(CD)=(AC)/(CE)`

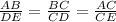
Now, consider the proportion of sides,

`(AB)/(DE)=(BC)/(CD)\\AB=(BC)/(CD)* DE\\AB=(60)/(24)* 18\\AB=(60* 18)/(24)=45\ ft`

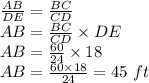
Therefore, the distance between A and B is 45 ft.