Question

A rope of negligible mass is wrapped around a 225-kg solid cylinder of radius 0.400 m. The cylinder is suspended several meters off the ground with its axis oriented horizontally, and turns on that axis without friction.

a) If a 75.0-kg man takes hold of the free end of the rope and falls under the force of gravity, what is his acceleration?

b) What is the angular acceleration of the cylinder?

c) If the mass of the rope were not neglected, what would happen to the angular acceleration of the cylinder as the man falls?

Ok for a) I do not understand why it wouldn't just be the acceleration due to gravity, and b) my answer I got is off by more than 10% so idk what I am doing wrong

so someone PLEASE help!!! Explicitly describing each step would be much appreciated!

Answer 1

a)6.67 m/s2

b)16.7 rad/s2

c)increasing angular acceleration

Step-by-step explanation:

a) It's because the system is not just mass of the man, it consists of the man holding a rope wrapped around a cylinder, not just a man free falling. So you would have to consider the rotating cylinder under the torque created by the man gravity force.

Let g = 10m/s2

T = mgd =75*10*0.4 = 300 N.m

The from the mass moments inertial of the solid cylinder:

`I = (Mr^2)/(2) = (225*0.4^2)/(2) = 18 kgm^2`

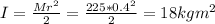
we can calculate the angular acceleration of the cylinder:

`\alpha = (T)/(I) = (300)/(18) = 16.7 rad/s^2`

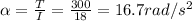
then translate that to acceleration:

`a = \alpha * r = 16.7*0.4 = 6.67 m/s^2`

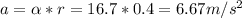
c) if the mass of the rope is not neglected, that means the force of gravity increases as the rope unwrapping around the cylinder, so the torque increases. Also the moment of inertial of the rope-cylinder system decreases due to rope unwrapping. In the end, the angular acceleration is no longer constant, but increasing.