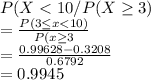Answer:
0.93471,0.02674,0,0.9945
Explanation:
giventhat web crawlers need to estimate the frequency of changes to Web sites to maintain a current index for Web searches.
X the changes to a web site is a Poisson variable with mean = 3.5 days
a) the probability that the next change occurs in less than 20 days
=
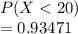
b) the probability that the time until the next change is greater 7.0 days
=

c) P(X>c) =0.90
Only for c=0 this is true.
d) the probability that the next change occurs in less than 10.0 days, given that it has not yet occurred after 3.0ays
=