To solve the problem it is necessary to apply the concepts related to angular resolution or spatial resolution, that is, it refers to the power of an instrument to separate two objects from an image.
The optical limit due to diffraction can be empirically calculated from the Rayleigh cemetery, where
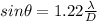
Where,
D = Diameter
 Eye
Eye
 = Wavelength
= Wavelength
Replacing our values then we have to
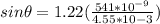
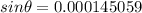
For small angles we have that
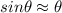
From the trigonometric definition of Sin? We have to

Where
d = Distance between lights
L = Length
Then,

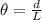
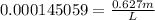

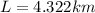
Therefore the distance, in kilmeters, you are able to discern that there are two headlights rather than a single light source is 4.322km