Question

14. A right-angled triangle LMN is shown below.

LN = 16.9 cm and LM = 6.5 cm.
16.9 cm
6.5 cm
МІ
Diagram not drawn to scale
Calculate the length MN.​

Answer 1

The Length of MN is 15.6 cm.

Explanation:

Given:

A right angled triangle LMN at angle M is equal to 90°

LN = Hypotenuse = 16.9 cm

LM = Shorter leg = 6.5 cm

To Find:

MN = Longer leg = ?

Solution:

In Right Angled Triangle Δ LMN

Pythagoras Theorem States that

`(\textrm{Hypotenuse})^(2) = (\textrm{Shorter leg})^(2)+(\textrm{Longer leg})^(2)`

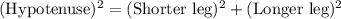
By applying Pythagoras theorem we get

`l(LN)^(2)= l(LM)^(2)+l(MN)^(2) \\\textrm{substituting the given values  of we get}\\\\16.9^(2)= 6.5^(2)+ (MN)^(2)\\ \therefore (MN)^(2)=285.61-42.25\\l(MN)^(2)=243.36\\l(MN)=\pm √(243.36)\\l(MN)=15.6\ cm .........\textrm{as distance cannot be in negative}`

The Length of MN is 15.6 cm.