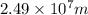Answer:
The radius of orbit=
Step-by-step explanation:
We are given that
Orbital speed=
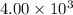 m/s
m/s
We have to find the radius of orbit of spacecraft.
We know that
Gravitational constant=
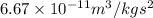
Mass of earth=
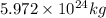
Orbital speed=
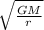
Where G= Gravitational constant
M=Mass of earth
r=Radius of orbit
Substitute the values in the formula
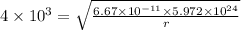
Squaring on both sides
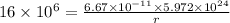
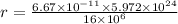
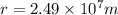
Hence, the radius of orbit=