Question

In a single growing season at the smith family orchard, the average yield per apple tree is 150 apples when the number of trees per acre is 100. For each additional tree over 100, the average yield per tree decreases by 1.

What would be the average yield per tree of the number of trees per acre was doubled? What would be the total yield in that case?

How many trees should be planted per acre to maximize the total yield?

Answer 1

100 trees should be planted per acre to maximize the total yield (15000 apples per acre)

Explanation:

Functions

Expressing some quantities in terms of other(s) comes in handy to understand the behavior of the situations often modeled by those functions.

Our problem tells us about the smith family orchard, where the average yield per apple tree is 150 apples when the number of trees per acre is 100 (or less). But the average yield per tree decreases when more than 100 trees are planted. The rate of decrease is 1 for each additional tree is planted

Let's call x the number of trees planted per acre in a single growing season. We have two conditions when modeling: when x is less than 100, the average yield per apple tree (Ay) is (fixed) 150.

`Ay(x)=150\ ,\ x\leqslant 100`

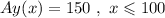
When x is more than 100:

`Ay(x)=150-x\ ,\ 100< x\leqslant 150`

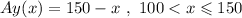
The upper limit is 150 because it would mean the Average yield is zero and no apples are to be harvested

Part 1

We are asked what happens if the number of trees per acre was doubled, but we don't know what the original number was. Let's make it x=60

If x=60, then we must use the first function, and

Ay(60)=150

The yield per acre will be 150*60=9000 apples

If we doubled x to 120, we would have to use the second function

Ay(120)=150-x=30

The yield per acre will be 30*120=3600 apples

Note that doubling the number of trees would make the production decrease

If we started with x=30, then

Ay(30)=150, and we would have 150*30=4500 apples per acre

We already know that for x=60 (the double of 30), our production will be 9000 apples per acre

This shows us that in some cases, increasing the number of trees is beneficial and in other cases, it is not

Part 2

The total yield is computed as

Y(x)=x.Ay(x)

This function will be different depending on the value of x

`Y(x)=150x\ ,\ x\leqslant 100`

`Y(x)=150x-x^2\ ,\ 100< x\leqslant 150`

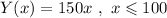
To find the maximum total yield we take the first derivative

`Y'(x)=150\ ,\ x\leqslant 100`

`Y'(x)=150-2x\ ,\ 100< x\leqslant 150`

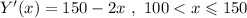
The first expression has no variable, so the total yield must be evaluated in the endpoints

Y(0)=0

Y(100)=15000

Now, the second expression contains variable, it will be set to 0 to find the critical point

150-2x=0

x=75

x is outside of the boundaries, we cannot find the maximum in this interval

Answer: 100 trees should be planted per acre to maximize the total yield (15000 apples per acre)