Answer:
The values are
a = -13
b = -84
Explanation:
Given:
z=6-7i and
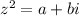
To Find:
a = ?
b = ?
Solution:
Z is Complex Number consist of Real part and Imaginary part
We have
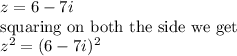
Using the identity
 we get
we get
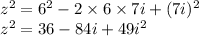
i² = -1
∴
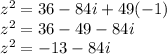
Now on comparing with
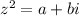 equation we get
equation we get
a = -13
b = -84