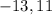Answers:
The absolute value of a real number (also called modulus) is a "non-negative value of that number without regard to its sign". This is because absolute values are, in fact, distances.
In other words: An absolute value is a number's distance from zero in the Number line, and are solved in the following way:
a)
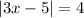
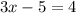
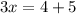

or
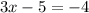
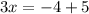
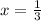
The value of
 is between
is between
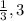
b)
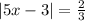
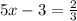
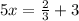
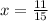
or
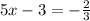

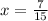
The value of
 is between
is between

c)
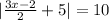
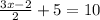
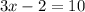

or

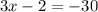
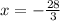
The value of
 is between
is between
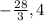
d)
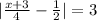
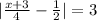
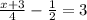
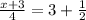
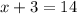
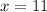
or
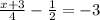
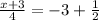

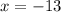
The value of
 is between
is between