The rational roots of the given equation are -4, -1, 2
Solution:
Given, equation is:
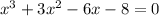
We have to find the rational root of the given cubic equation.
Now, let us try it by trail and error method.
So, put x = 1 in given
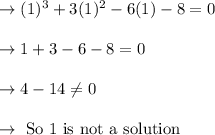
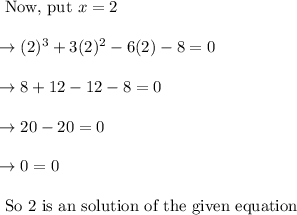
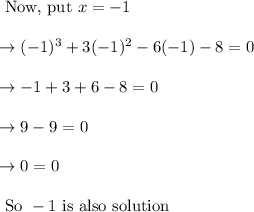
Now we have got two roots 2 and – 1
We can find the third root by formula sum of roots
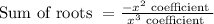
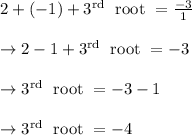
Hence, the rational roots of the given equation are -4, -1, 2