Question

What is the rational root of x^3+3x^2-6x-8=0

Answer 1

The rational roots of the given equation are -4, -1, 2

Solution:

Given, equation is:

`x^(3)+3 x^(2)-6 x-8=0`

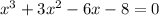
We have to find the rational root of the given cubic equation.

Now, let us try it by trail and error method.

So, put x = 1 in given

`\begin{array}{l}{\rightarrow(1)^(3)+3(1)^(2)-6(1)-8=0} \\\\ {\rightarrow 1+3-6-8=0} \\\\ {\rightarrow 4-14 \\eq 0} \\\\ {\rightarrow \text { So } 1 \text { is not a solution }}\end{array}`

`\begin{array}{l}{\text { Now, put } x=2} \\\\ {\rightarrow(2)^(3)+3(2)^(2)-6(2)-8=0} \\\\ {\rightarrow 8+12-12-8=0} \\\\ {\rightarrow 20-20=0} \\\\ {\rightarrow 0=0} \\\\ {\text { So } 2 \text { is an solution of the given equation }}\end{array}`

`\begin{array}{l}{\text { Now, put } x=-1} \\\\ {\rightarrow(-1)^(3)+3(-1)^(2)-6(-1)-8=0} \\\\ {\rightarrow-1+3+6-8=0} \\\\ {\rightarrow 9-9=0} \\\\ {\rightarrow 0=0} \\\\ {\text { So }-1 \text { is also solution }}\end{array}`

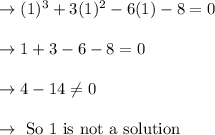
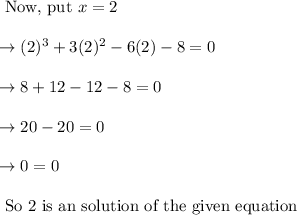
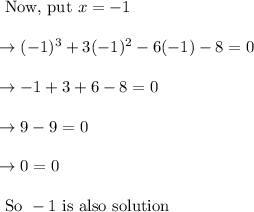
Now we have got two roots 2 and – 1

We can find the third root by formula sum of roots

`\text {Sum of roots }=\frac{-x^(2) \text { coefficient }}{x^(3) \text { coefficient }}`

`\begin{array}{l}{2+(-1)+3^{\text {rd }} \text { root }=(-3)/(1)} \\\\ {\rightarrow 2-1+3^{\text {rd }} \text { root }=-3} \\\\ {\rightarrow 3^{\text {rd }} \text { root }=-3-1} \\\\ {\rightarrow 3^{\text {rd }} \text { root }=-4}\end{array}`

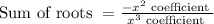
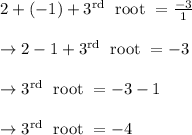
Hence, the rational roots of the given equation are -4, -1, 2