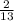Answer:
Probability of drawing a 7 or an 8 is
Explanation:
Total number of cards in the given deck = 52
Now, the number of 7 in the deck = 4
Also, the number of 8 in the deck = 4
So, the total number of ( 7 + 8) in the deck = 4 + 4 = 8 cards
Let E: Event of picking a 7 or an 8
Here, the total number of favorable outcomes = 8
Now,
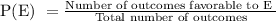
So, here
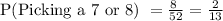
or, P(Picking a 7 or 8) = 2/13
Hence, The probability of drawing a 7 or an 8 is