Question

A stone is thrown straight up from earth with D(t)= -4.9 t^2 + vt where D = height in meters, t= time in seconds, and v= initial speed in m/s. Find the following:

(a) D(t) ?
(b) the time in the air ?
(c) the maximum height ?
(d) the instantaneous velocities at t= a, and t= b?
(e) the average velocity from t= a to t= b?
(f) the velocity of the stone as it runs into the ground ?
(g) the total ground distance traveled ?
+ (For initial speed = 49 m/s, a= 4 sec, b= 9 sec.)

Answer 1

(a) D(t)= -4.9 t^2 + vt

(b) 10 sec

(c) 122.5m

(d) At t= 4sec, v= 9.8m/s (upwards) and at t= 9sec, v= 39.2m/s (downwards)

(e) -24.5m

(f) -49m/s (i.e. downwards)

(g) 0

Explanation:

(b) Time in the air = 2v/g = 10sec

(c) Maximum height =
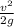`(v^(2) )/(2g)` =122.5m

(d) Velocity at any time t = v -9.8t

So, at t= 4sec, velocity = 49 – 9.8(4) =9.8m/s

at t= 9sec, velocity = 49 – 9.8(9) = -39.2m/s

(e) Average velocity =
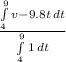`\frac{\int\limits^9_4 {v-9.8t} \, dt }{\int\limits^9_4 {1} \, dt }` = -24.5m

(g) the stone is thrown vertically upwards, so no horizontal distance covered.