Answer:
2578.99 years
Step-by-step explanation:
Given that:
100 g of the wood is emitting 1120 β-particles per minute
Also,
1 g of the wood is emitting 11.20 β-particles per minute
Given, Decay rate = 15.3 % per minute per gram
So,
Concentration left can be calculated as:-
C left =
![[A_t]=(11.20\ per\ minute)/(15.3\ per\ minute\ per\ gram)* [A_0]= 0.7320[A_0]](https://img.qammunity.org/2020/formulas/chemistry/college/x4htq82jrcjv54rwdnq4pzfejq0x577qaf.png)
Where,
![[A_t]](https://img.qammunity.org/2020/formulas/chemistry/college/wbj92t0z4axifcyqa24z3ary269op2iva8.png) is the concentration at time t
is the concentration at time t
![[A_0]](https://img.qammunity.org/2020/formulas/chemistry/college/izynxfnwyud2ghdog9l8ny0mhzwshbud6r.png) is the initial concentration
is the initial concentration
Also, Half life of carbon-14 = 5730 years
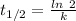
Where, k is rate constant
So,
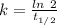
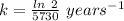
The rate constant, k = 0.000120968 year⁻¹
Time =?
Using integrated rate law for first order kinetics as:
![[A_t]=[A_0]e^(-kt)](https://img.qammunity.org/2020/formulas/chemistry/college/wgh5hifj7f12vitsa51kophgqrxxcfit2c.png)
So,
![\frac {[A_t]}{[A_0]}=e^(-0.000120968* t)](https://img.qammunity.org/2020/formulas/chemistry/college/evwmj76z9t6d8t3b3qav6qg1bvacr10mfe.png)
![\frac {0.7320[A_0]}{[A_0]}=e^(-0.000120968* t)](https://img.qammunity.org/2020/formulas/chemistry/college/qk6pc0w3ghsgxvtawf2e64ygw0qkn7kp4c.png)
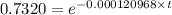
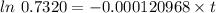
t = 2578.99 years