Question

For each student in a certain class, a teacher adjusted the student's test score using the formula y = 0.8x + 20, where x is the student's original test score and y is the student's adjusted test score. If the standard deviation of the original test scores of the students in the class was 20, what was the standard deviation of the adjusted test scores of the students in the class? A. 12 B. 16 C. 28 D. 36 E. 40

Answer 1

Option B) 16

Explanation:

We are given the following in the question:

`y = 0.8x + 20`

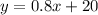
where x is the student's original test score and y is the student's adjusted test score.

We have to find the standard deviation of the adjusted test scores of the students in the class, if the standard deviation of the original test scores of the students in the class was 20.

We know that:

• Adding a constant to each value in a data set does not change the value of the standard deviation.
• Multiplying each value in a data set by a constant also multiplies the standard deviation by that constant.

Thus, if we add 20 to each data set then, the standard deviation does not change.

But multiplying each score by 0.8, changes the standard deviation 0.8 times.

Thus, we can write:

`\text{Standard deviation of the adjusted test scores}\\ = \text{Standard deviation of the original test scores of the students}* 0.8\\= 20* 0.8\\= 16`

Thus, standard deviation of adjusted score is 16.