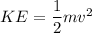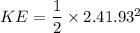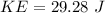Question

A 24.1 N solid sphere with a radius of 0.151 m is released from rest and rolls, without slipping, 1.7 m down a ramp that is inclined at 34o above the horizon. What is the total kinetic energy of the sphere at the bottom of the ramp?What is the angular speed of the sphere at the bottom of the ramp? How many radians did the sphere rotate through as it rolled down the ramp What was the angular acceleration of the sphere as it rolled down the ramp

Answer 1

given,

weight of solid sphere = 24.1 N

m = 24.1/g = 24.1/10 = 2.41 Kg

radius = R = 0.151 m

height of the ramp = 1.7 m

angle with horizontal = 34°

acceleration due to gravity = 10 m/s²

using energy conservation

`(1)/(2)I\omega^2 + (1)/(2)mv^2 = mgh`

I for sphere

`I = (2)/(5)mr^2` v = r ω

`(1)/(2)\ (2)/(5)mr^2* (v^2)/(r^2) + (1)/(2)mv^2 = mgh`

`(7)/(10)mv^2 = mgh`

`h = (0.7 v^2)/(g)`

`v = \sqrt{(h * g)/(0.7)}`

`v = \sqrt{(1.7 * 10)/(0.7)}`

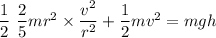
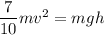
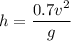
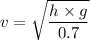
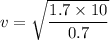
v = 4.93 m/s

b) rotational kinetic energy

`KE=(1)/(2)I\omega^2`

`KE=(1)/(2)\ (2)/(5)mr^2* (v^2)/(r^2)`

`KE=(1)/(5)mv^2`

`KE=(1)/(5)* 2.41 * 4.93^2`

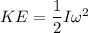
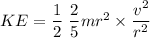
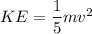
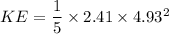
KE = 11.71 J

c) Translation kinetic energy

`KE=(1)/(2)mv^2`

`KE=(1)/(2)* 2.41 \time 4.93^2`

`KE=29.28\ J`