Question

Problem 5 You are playing a game where you drop a coin into a water tank and try to land it on a target. You often find this game at fast food places as part of a fundraiser. The sides of the tank are flat and the target is 6in from the side of the tank. Your eye is 9in from the side of the tank. Water has index of refraction of 4/3. Because of light refraction at the interface, the target appears, to your eye, to be at a different position than its true position. If you drop the coin accurately and it falls straight down to the location where the target appears to be, how far are you off? Does the coin fall in front or behind the target as you look at it? Select One of the Following: (a) 0.75in behind the target. (b) 1.5in behind the target. (c) 0.75in in front of the target. (d) 1.5in in front of the target

Answer 1

Option D: 1.5in in front of the target

Step-by-step explanation:

The object distance is
`y= 6in`.

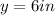Because the surface is flat, the radius of curvature is infinity .

The incident index is
`n_i=(4)/(3)` and the transmitted index is
`n_t= 1`.

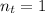The single interface equation is
`(n_i)/(y)+(n_t)/(y^i)=(n_t-n_i)/(r)`

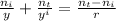
Substituting the quantities given in the problem,

`((4)/(3))/(6in)+(1)/(y^i)= 0`

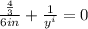
The image distance is then
`y^i=-(18)/(4)in =-4.5in`

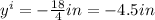
Therefore, the coin falls
`1.5in` in front of the target