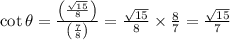2 Answers

Umesh · Answer 1 · 2020-02-12T12:16:06+0000

Out of the given choice, the equation represents
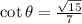$\cot \theta=(√(15))/(7)$ .

Answer: Option B

Explanation:

We know,
$\csc \theta=(1)/(\sin \theta)$

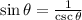
$\sin \theta=(1)/(\csc \theta)$

Given data:

$\csc \theta=(8)/(7)$

So, now sin theta can express as

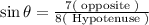
$\sin \theta=\frac{7(\text { opposite })}{8(\text { Hypotenuse })}$

Sin theta defined by the ratio of opposite to the hypotenuse. In general, the adjacent can be calculated by,

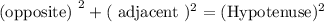
$\text {(opposite) }^(2)+(\text { adjacent })^(2)=(\text {Hypotenuse})^(2)$

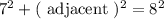
$7^(2)+(\text { adjacent })^(2)=8^(2)$

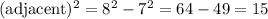
$(\text {adjacent})^(2)=8^(2)-7^(2)=64-49=15$

Taking square root, we get

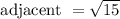
$\text { adjacent }=√(15)$

Also, we know the formula for cot theta,

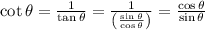
$\cot \theta=(1)/(\tan \theta)=(1)/(\left((\sin \theta)/(\cos \theta)\right))=(\cos \theta)/(\sin \theta)$

Cos theta denoted as the ratio of adjacent to the hypotenuse.

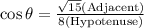
$\cos \theta=\frac{√(15)(\text {Adjacent})}{8(\text {Hypotenuse})}$

Therefore, find now as below,

$\cot \theta=(\left((√(15))/(8)\right))/(\left((7)/(8)\right))=(√(15))/(8) * (8)/(7)=(√(15))/(7)$

Please log in or register to add a comment.