Answer:
The point M is (10,7.5).
Explanation:
Given:
AB is in a ratio of 5:5. A is at (0, 15) and B is at (20,0).
Now, to find the point M that divides the segment AB.
The points are A (0,15) and B (20,0) of the segment AB, which divides the point into
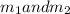 .
.
So,
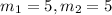 .
.
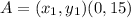 and
and

So, by putting the formula to find M.
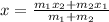
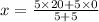
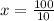
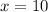
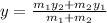



So, the required point is
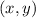 =(10,7.5)
=(10,7.5)
Therefore, the point M is (10,7.5).