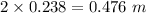Question

A child playing in a swimming pool realizes that it is easy to push a small inflated ball under the surface of the water while a large ball requires a lot of force. The child happens to have a styrofoam ball (this way the shape of the ball will not distort when it is forced under the surface) which is being forced under the surface of the water. If the child needs to supply 5.00 × 102 N to totally submerge the ball, calculate the diameter of the ball. The density of water is rhow = 1.000 × 103 kg/m3, the density of styrofoam is rhofoam = 95.0 kg/m3 and the acceleration due to gravity is g = 9.81 m/s2.

Answer 1

The diameter as calculated is 0.476 m

Solution:

As per the question:

Tension, T =
`5* 10^(2) = 500\ N`

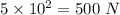
Density of water,
`1.00* 10^(3)\ kg/m^(3)`

Density of the styrofoam,
`\rho_(foam) = 95.0\ kg/m^(3)`

Now,

To calculate the diameter, d of the ball:

With the help of the Archimedes's principle:

At equilibrium, upthrust equals the weight of the displaced liquid.

where

Mass, m =
`V\rho` (1)

where

V = Volume of ball

`\rho = density`

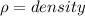
Force, F = mg

From eqn (1):

Force , F =
`V\rho_(w) g` (1)

Now,

Net downward force is given by:

F' = F + T =
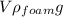`V\rho_(foam) g` + T (2)

Thus equating (1) and (2):

F = F'

`V\rho_(w)g = V\rho_(foam) g + T`

`V = {T}{(\rho_(w) - \rho_(foam))}`

`V = {500}{9.8(1.00* 10^(3) - 95.0)} = 0.056\ m^(3)`

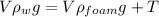
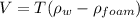
Also, we know that for ball:

`V = (4)/(3)\pi R^(3)`

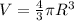
where

R = Radius of the ball

`0.056 = (4)/(3)\pi R^(3)`

R = 0.238 m

Since, radius is known, the diameter is twice the radius:

Diameter, d = 2R =
`2* 0.238 = 0.476\ m`