Question

Assume that the firework has a mass of m_0 = 0.30~\text{kg}m ​0 ​​ =0.30 kg and is launched from a cannon at an angle of \theta_0 = 39.7^\circθ ​0 ​​ =39.7 ​∘ ​​ with an initial velocity of | v_0 | = 20~\text{m/s}∣v ​0 ​​ ∣=20 m/s. Just as the firework reaches its hight point in its trajectory, it explodes into two pieces. Immediately after the explosion, the first piece, with a mass of m_1 = 0.2~\text{kg}m ​1 ​​ =0.2 kg flies off at an angle \theta_1 = 150^\circθ ​1 ​​ =150 ​∘ ​​ relative to the positive (forward) horizontal axis at a velocity of | v_1 | = 5~\text{m/s}∣v ​1 ​​ ∣=5 m/s relative to the ground. Calculate the trajectory angle, \theta_2θ ​2 ​​ of the second piece immediately after the explosion. Assume the second piece has a mass of m_2 = 0.1~\text{kg}m ​2 ​​ =0.1 kg, neglect the effect of air resistance, and report your result as an angle relative to the positive (forward) horizontal axis.

Answer 1

The expression for the initial velocity of the cannon ball is:
`v_i= (v_i cos\theta_i)x + (v_i sin\theta_i)y`

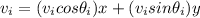
The expression for the initial velocity of the piece-1 after the collision is:

`v_i=(v_i sin\theta'(-x) + (v_i cos\theta')y`

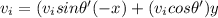
The expression for the angle is:

`\theta' -90^o`

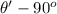
Then the expression for the initial velocity of the piece-1 after the collision is:

`v_i= (v_i sin\theta')(-x) + (v_icos\theta')y\\\\= -(v_i sin (\theta_1 -90^o))x + (v_1 cos(\theta_1 —90^o))y`

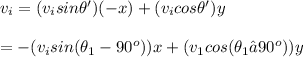
The expression for the initial velocity of the piece-2 after the collision is:

`v_2=(v_2 cos\theta_2 ) x + (v_2 sin\theta_2)(-y)\\\\= (v_2 cos\theta_2)x- (v_2 sin\theta_2)y`

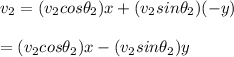
The expression for the law of conservation of momentum for the cannon ball and the two pieces is

`m_(c)v_(i) = m_(1)v_(1)+m_(2)v_(2)\\\\=m_c ((v_1cos\theta_1)x+(v_1sin\theta_1)y)=m_1(-(v_1 sin(\theta_1-90^o))x+(v_1cos(\theta_1-90^o))y)+m_2( (v_2cos\theta_2)x-(v_2sin\theta_2)y)\\\\=(m_cv_1cos\theta_1)x+(m_cv_1v_1sin\theta_1)y=((m_2v_2 cos(\theta_2)-m_1v_1sin(\theta_1-90^o)))x+((m_1v_1cos(\theta_1-90^o))-(m_2v_2sin\theta_2))y`

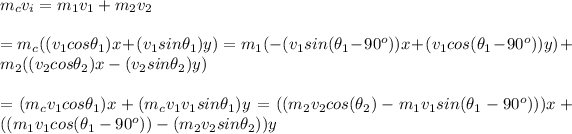
Compare the x and y-components of the above equation as follows:

`(m_2v_2 cos\theta_2)-(m_1v_1 sin (\theta_1 —90^o))= m_cv_icos \theta_1\\\\ m_2v_2 cos\theta_2=m_1v_1 sin (\theta_1 —90^o)+m_cv_icos \theta_1.........(1)\\\\m_1v_1 cos (\theta_1 —90^o))- (m_2v_2 sin\theta_2)=m_cv_isin \theta_1\\\\m_2v_2 sin\theta_2=m_1v_1 cos (\theta_1 —90^o)+m_cv_isin\theta_1.........(2)`

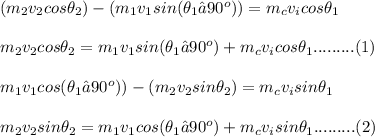
Square and add equations (1) and (2) as follows:

`(m_2v_2cos\theta_2)^2=(m_1v_1sin(\theta_1-90^o)+m_cv_1cos\theta_1)^2+(m_2v_2sin\theta_2)^2=(m_1v_1cos(\theta_1-90^o)+m_cv_1sin\theta_1)^2\\\\=(m_2v_2)^2=(m_1v_1sin(\theta_1-90^o)+m_cv_1cos\theta_1)^2+(m_1v_1cos(\theta_1 —90^o))-(m_cv_1sin\theta_1)^2\\\\v_2=(1)/(m_2)[tex]√((m_1v_1sin(\theta_1-90^o)+m_cv_1cos\theta_1)^2+(m_1v_1cos(\theta_1 —90^o))-(m_cv_1sin\theta_1)^2)`

Calculate the magnitude of the velocity of the piece-2 as follows