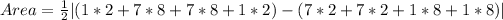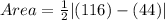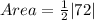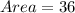Question

Find the perimeter and the area of the polygon with the given vertices. J (1,2), K (7,2), L (7,8), M (1,8) The perimeter is units. The area is square units.

Answer 1

Perimeter = 24 units

Area = 36 units^2

Explanation:

Given

`J=(1,2)`

`K = (7,2)`

`L = (7,8)`

`M = (1,8)`

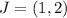
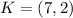
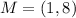
Required

Calculate the perimeter and the area

Calculating Perimeter:

First, we calculate the distance between each point.

For J and K

`J=(1,2)`
`K = (7,2)`

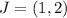
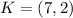
They have the same y value (i.e. 2); So, the distance is the difference between their x values:

`D_1 = |1-7|=|-6| = 6`

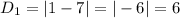
For K and L

`K = (7,2)`
`L = (7,8)`

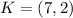
They have the same x value (i.e. 7); So, the distance is the difference between their y values:

`D_2 = |2-8| = |-6| = 6`

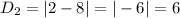
For L and M

`L = (7,8)`
`M = (1,8)`

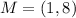
They have the same y value (i.e. 8); So, the distance is the difference between their x values:

`D_3 = |7-1| = |6| = 6`

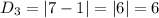
For M and J

`J=(1,2)`
`M = (1,8)`

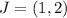
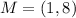
They have the same x value (i.e. 1); So, the distance is the difference between their y values:

`D_4 = |2-8| = |-6| = 6`

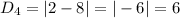
So, the perimeter (P) is:

`P = D_1 + D_2 + D_3 + D_4`

`P = 6 + 6 + 6 + 6`

`P = 24`

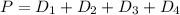
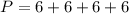
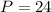
Calculating the Area

The area is calculated using:

`Area = (1)/(2)|(x_1y_2+x_2y_3+x_3y_4+x_4y_1) - (x_2y_1 + x_3y_2+x_4y_3+x_1y_4)|`

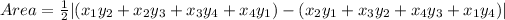
Where:

`J=(1,2)` --
`(x_1,y_1)`

`K = (7,2)` --
`(x_2,y_2)`

`L = (7,8)` --
`(x_3,y_3)`

`M = (1,8)` --
`(x_4,y_4)`

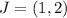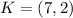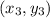
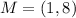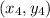
So, we have:

`Area = (1)/(2)|(1*2+7*8+7*8+1*2)-(7*2+7*2+1*8+1*8)|`

`Area = (1)/(2)|(116)-(44)|`

`Area = (1)/(2)|72|`

`Area = (1)/(2)*72`

`Area = 36`