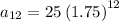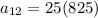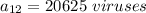Answer:
Chris will find 20625 viruses in 12 hours
Explanation:
Geometric Progressions
The geometric progression can be understood as a sequence or ordered terms when the term n equals the previous term n-1 by a constant value called the common ratio

Recursively going back we find that
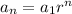
Being
 the first term of the sequence
the first term of the sequence
Chris' experiment shows that viruses grow at a rate of 75% per hour. It means that we get the next generation of viruses as the previous by 1.75. This is the common ratio. We also know he starts his experiment with 25 viruses, this makes
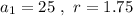
We can now express the number of viruses as a function of the number of hours n:

We are required to compute the number of viruses found when n=12 hours: