Question

Do you length of a rectangle is five times the width. If the length and width are both increased by 2, the new area would be 85. What is the original area?

Answer 1

The original of the given rectangle = 45 sq units.

Explanation:

Here, let us assume the actual width of the rectangle = a

So, the actual length of the rectangle = 5 x ( width) = 5 (a) = 5 a

Now, the new width w' = ( a + 2)

and the new length l' = ( 5 a + 2)

AREA OF THE RECTANGLE = LENGTH x WIDTH

So, the area of the new rectangle = (a + 2)(5 a +2)

Also, new area = 85 ⇒(a + 2)(5 a +2) = 85

`\implies 5a^2 + 10 a + 2a + 4 = 85\\\implies 5a^2 + 12a - 81 = 0\\\implies 5a^2 - 15 a + 27 a - 81 = 0\\\implies 5a(a -3) + 27(a -3) = 0\\\implies (5a +27)(a-3)= 0`

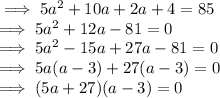
⇒ ( 5a +27) =0 or (a-3) = 0

⇒ a = -27/5 or a = 3

But, a = Width of a rectangle , so a CANNOT be Negative

⇒ a ≠ -27/5 and a = 3

So, the actual width of the rectangle = a = 3

The length of the rectangle = 5 a = 5 (3) = 15

The original area = Original L x Original W = 3 x 15 = 45 sq units.