Answer:
54.80 MPa to 55.92 MPa
Explanation:
Sample mean fracture strength (x) = 55.36 MPa
Sample standard deviation (s) = 3.99 MPa
Sample size (n) = 196.
The upper and lower bounds for a 95% confidence interval are given by:
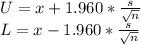
The upper and lower bounds of the confidence interval are;
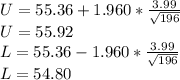
The 95% confidence interval for true average fracture strength is 54.80 MPa to 55.92 MPa