Question

Help Please!!

Two cards are dealt from the top of a well-shuffled standard deck of cards.

a. Draw a tree diagram showing the probabilities of a heart (H) and non-heart (N) for each of the two cards.

b. Find P(HH), P(HN), P(NH), and P(NN).


(Only need help with b!)

Answer 1

`P(HH)=(13)/(52) (12)/(51)=0.0588`

`P(HN)=(13)/(52) (39)/(51)=0,1912`

`P(NH)=(39)/(52) (13)/(51)=0,1912`

`P(NN)=(39)/(52) (38)/(51)=0,5588`

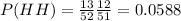
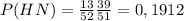
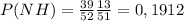
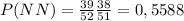
Explanation:

Probabilities with events without replacement

When a random experience is performed without replacement, it means the conditions for the first and subsequent observations are not the same, the sample space changes. The throw of a die is an example of a random experience with replacement since each throw is done with the same die in the same conditions. Taking two cards from a deck of cards is a non-replacing experience.

b)

In the random experience described in the question, two cards are dealt from a deck of cards. The first card is taken from a deck of 52 cards, the second from a deck of 51 cards. We are observing if the card is a Heart (H) or a non-heart (N). Four things can happen:

HH -> Two hearts are dealt

HN -> First card is a Heart, the second card is a non-heart

NH -> First card is a non-heart, the second card is a Heart

NN -> Two non-hearts are dealt

Case 1: HH

The first Heart is taken from 10 available. The probability of that event is
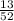`(13)/(52)`. The second heart is taken from 9 available out of 51 cards. The probability is
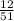`(12)/(51)`. The combined probability is the product of both

`P(HH)=(13)/(52) (12)/(51)=0.0588`

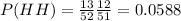
Case 2: HN

The probability of H in the first deal is already computed:
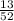`(13)/(52)`. The second card is a non-heart, which can be taken from all the non-heart cards available, 39 in total. So the probability of taking a non-heart is
`(39)/(51)`

`P(HN)=(13)/(52) (39)/(51)=0,1912`

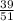
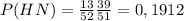
Case 3: NH

The probability of taking a non-heart as the first card is
`(39)/(52)`. The second card is a heart, taken from the remaining 13 with probability
`(13)/(51)`

`P(NH)=(39)/(52) (13)/(51)=0,1912`

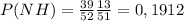
Case 4: NN

Similar reasoning leads to

`P(NN)=(39)/(52) (38)/(51)=0,5588`

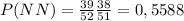
Notice all of them sum 1