Question

In a test of the effectiveness of garlic for lowering​ cholesterol, 42 subjects were treated with garlic in a processed tablet form. Cholesterol levels were measured before and after the treatment. The changes ​(beforeminus​after) in their levels of LDL cholesterol​ (in mg/dL) have a mean of 3.4 and a standard deviation of 18.2. Construct a 90​% confidence interval estimate of the mean net change in LDL cholesterol after the garlic treatment. What does the confidence interval suggest about the effectiveness of garlic in reducing LDL​ cholesterol?

Answer 1

90% Confidence interval: (-1.21,8.01)

Explanation:

We are given the following information in the question:

Sample size, n = 42

Sample mean = 3.4

Sample standard Deviation = 18.2

90% Confidence interval:

`\mu \pm z_(critical)(\sigma)/(√(n))`

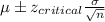
Putting the values, we get,

`z_(critical)\text{ at}~\alpha_(0.10) = \pm 1.645`

`3.4 \pm 1.645((18.2)/(√(42)) ) = 3.4 \pm 4.61 = (-1.21,8.01)`

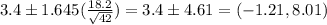
Since, the confidence interval limits contain 0, suggesting that the garlic treatment did not affect the LDL cholesterol levels.