Question

Conduct a hypothesis test to determine, at the significance level 0.01, whether there is reason to believe that the true percentage of those in the first group who suffer a second episode is different from the true percentage of those in the second group who suffer a second episode? Select the [Alternative Hypothesis, Value of the Test Statistic].

Answer 1

Alternative hypothesis is
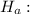`H_(a):` p1≠p2. Test Statistic is 0.1928.

There is no significant evidence to believe that the true percentage of those in the first group who suffer a second episode is different from the true percentage of those in the second group who suffer a second episode at 0.01 significance level.

Explanation:

The Question is missing. Full question is as follows:

It has been observed that some persons who suffer acute heartburn, again suffer acute heartburn within one year of the first episode. This is due, in part, to damage from the first episode. The performance of a new drug designed to prevent a second episode is to be tested for its effectiveness in preventing a second episode.In order to do this two groups of people suffering a first episode are selected. There are 55 people in the first group and this group will be administered the new drug. There are 75 people in the second group and this group will be administered a placebo. After one year, 10% of the first group has a second episode and 9% of the second group has a second episode. Conduct a hypothesis test to determine, at the significance level 0.01,whether there is reason to believe that the true percentage of those in the first group who suffer a second episode is different from the true percentage of those in the second group who suffer a second episode? Select the [Alternative Hypothesis, Value of the Test Statistic].

Let p1 be the proportion of the first group who has second episode

Let p2 be the proportion of the second group who has second episode

`H_(0): p1=p2`

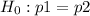
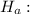`H_(a):` p1≠p2

z-statistic of the test can be found using the formula

z=
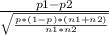`\frac{p1-p2}{\sqrt{(p*(1-p)*(n1+n2))/(n1*n2) } }` where

• p1 is the sample proportion of the first group who has second episode (0.1 or 10%)

• p2 is the sample proportion of the second group who has second episode(0.09 or 9%)

• p is the pool proportion of p1 and p2 (
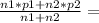  `(n1*p1+n2*p2)/(n1+n2) =`0.09423)

• n1 is the sample size of the first group (55)

• n2 is the sample size of the second group (75)

Then

z=
`\frac{0.10-0.09}{\sqrt{(0.09423*0.90577*(55+75))/(55*75) } }`

≈ 0.1928 corresponding two tailed p-value p(z) is 0.8471.

Since p(z)>0.1 we fail to reject the null hypothesis and conlude that p1=p2 at 0.01 significance.