Question

A 1.80-kg monkey wrench is pivoted 0.250 m from its center of mass and allowed to swing as a physical pendulum. The period for small-angle oscillations is 0.940 s.

Answer 1

Moment of inertia,
`I = 0.0987\ kg-m^2`

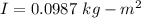
Step-by-step explanation:

It is given that,

Mass of the monkey, m = 1.8 kg

Distance from the center of mass, d = 0.25 m

The time period of oscillation, t = 0.94 s

It is assumed to find the moment of inertia of the wrench about an axis through the pivot. the time period of the oscillation is given by :

`t=2\pi \sqrt{(I)/(mgd)}`

`I=(mgdt^2)/(4\pi^2)`

`I=(1.8* 9.8* 0.25* (0.94)^2)/(4\pi^2)`

`I = 0.0987\ kg-m^2`

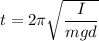
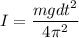
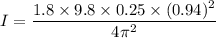
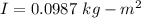
So, the moment of inertia of the wrench about an axis through the pivot is
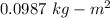`0.0987\ kg-m^2`. Hence, this is the required solution.