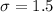Answer:
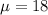 and
and
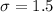
Explanation:
Let
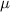 = mean and
= mean and
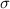 = standard deviation.
= standard deviation.
Given : If a set of data are normally distributed with at least 68% of scores falling between scores 16.5 and 19.5.
If these values mark the first standard deviation from the mean, then
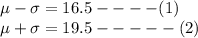
Adding (1) and (2) ,we get
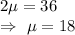
Subtract (1) from (2) , we get
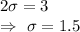
Hence, the values of the mean and standard deviation in this normal distribution are :
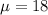 and
and