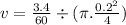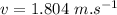Question

You work for the city water department and need to pump 3400 liters/minute of water from a tank at ground level into a vented (i.e., open-top) water tower, 75 meters above ground. The pump can be considered adiabatic, and the combined efficiency of pump and its drive motor is 90 percent. Determine: the electric power required (kW) to drive the pump if friction losses are neglected and the average velocity (m/s) of the water if a 20-cm diameter (ID) pipe is used.

Answer 1

`P_E=46.2778\ kW`

`v=1.804\ m.s^(-1)`

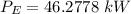
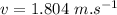
Step-by-step explanation:

Given:

• flow rate of water,
  `\dot{V}=3400\ L.min^(-1)=3.4\ m^3.min^(-1)`

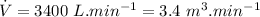
∵Density of water is 1 kg per liter

∴mass flow rate of water,
`\dot{m}=3400\ kg.min^(-1)`

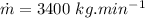
• height of pumping,
  `h=75\ m`

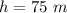
• efficiency of motor drive,
  `\eta=0.9`

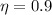
• diameter of pipe,
  `D =0.2\ m`

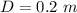
Now the power required for pumping the water at given conditions:

`P=\dot{m}.g.h`

`P=(3400)/(60) * 9.8* 75`

`P=41650\ W`

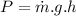
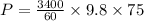
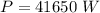
Hence the electric power required:

`P_E * \eta=P`

`P_E * 0.9=41650`

`P_E=46.2778\ kW`

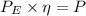
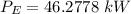
Flow velocity is given as:

`v=\dot{V}/ a`

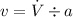
where: a = cross sectional area of flow through the pipe

`v=(3.4)/(60)/ (\pi.(0.2^2)/(4) )`

`v=1.804\ m.s^(-1)`