Question

A chemist wants to extract a solute from 100 mL of water using only 300 mL of ether. The partition coefficient between ether and water is 3.10 . Calculate q , the fraction of solute that would remain in the water under each of the extraction conditions. a) A single extraction with 300 mL of ether.b) Three extractions with 100 mL of ether.c) Six extractions with 50 mL of ether.

Answer 1

a. 0,903

b. 0,985

c. 0,996

Step-by-step explanation:

Partition coefficient between ether and water is:

`K = (CONCether)/(CONCwater)`

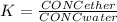
a. As k = 3,10, a single extraction with 300mL ether will give:

`3,10 = ((q/300mL))/((1-q)/100mL)`

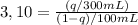
9,30 - 9,30q = q

9,30 = 10,30q

q = 0,903

b. Three extractions of 100 mL will extract:

First extraction:

`3,10 = ((q/100mL))/((1-q)/100mL)`

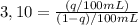
3,10 - 3,10q = q

3,10 = 4,10q

q = 0,756

The second extraction will 0,756 times of the solute that is in water. This solute is 1-0,756=0,244

Second extraction will extract 0,244*0,756 = 0,184

In the same way, third extraction will extraxt: (0,244-0,184)*0,756 = 0,045

Total solute extracted:

q = 0,756 + 0,184 + 0,045 = 0,985

c. Six extractions with 50mL of ether extract:

First extraction:

`3,10 = ((q/50mL))/((1-q)/100mL)`

3,10 - 3,10q = 2q

3,10 = 5,10q

0,608 = q

Second extraction = (1-0,608)*0,608 = 0,234

Third extraction =(1-0,608-0,234)*0,608 = 0,096

Fourth extraction =(1-0,608-0,234-0,096)*0,608 = 0,038

Fifth extraction =(1-0,608-0,234-0,096-0,038)*0,608 = 0,015

Sixth extraction =(1-0,608-0,234-0,096-0,038-0,015)*0,608 = 0,005

q = 0,608+0,234+0,096+0,038+0,015+0,005 = 0,996

I hope it helps!