Answer:
1.29 m/s ∠ 35.2°
Step-by-step explanation:
Let consider point A and C are in horizontal direction and the stream flows in vertical direction.
Horizontal Velocity:
The boat has to cross the river in 10 minutes and reach point C.
so Vi= 648.6/(10*60) m/s
Vi=1.08 m/s
Vertical Velocity:
The water will flow the boat in south direction, to reach point C the boat need to acquire same velocity in the opposite direction of river flow.
so
Vj= (2.54 km)/(1 hr) = (2.54*1000 m)/3600 sec
Vj= 0.706 m/s
Magnitude of Velocity:
V=
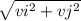
V=
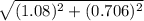
V=1.29 m/s
Direction of boat:
∅=
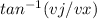
∅=
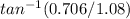
∅=35.2°