Question

Just about everyone at one time or another has been burned by hot water or steam. This problem compares the heat input to your skin from steam as opposed to hot water at the same temperature.

Assume that water and steam, initially at 100?C, are cooled down to skin temperature, 34?C, when they come in contact with your skin. Assume that the steam condenses extremely fast. We will further assume a constant specific heat capacity c=4190J/(kg?K) for both liquid water and steam.

How much heat H1 is transferred to the skin by 25.0 g of steam onto the skin? The latent heat of vaporization for steam is L=2.256

Answer 1

`Q_T=63313.5\ J`

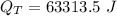
Step-by-step explanation:

Given:

• temperature of skin,
  `T_s=34^(\circ)C`

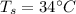
• initial temperature of steam vapour,
  `T_v=100^(\circ)C`

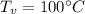
• latent heat of steam,
  `L=2256\ J.g^(-1)`

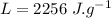
• mass of steam,
  `m=25\ g`

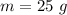
• specific heat of water,
  `c=4190\ J.kg^(-1).K^(-1)=4.19\ J.g^(-1).K^(-1)`

• final temperature,
  `T_f=34^(\circ)C`

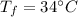
Assuming that no heat is lost in the surrounding.

We know:

`Q=m.c.\Delta T`

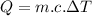
Now the total heat given by the steam to form water at the given conditions:

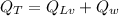`Q_T=Q_(Lv)+Q_w` ..............................(1)

where:

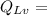`Q_(Lv)=` latent heat given out by vapour to form water of 100°C

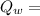`Q_w=` heat given by water of 100°C to come at 34°C.

putting respective values in eq. (1)

`Q_T=m(L+c.\Delta T)`

`Q_T=25(2256+4.19* 66)`

`Q_T=63313.5\ J`

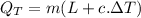
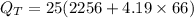
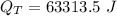
is the heat transferred to the skin.