Question

An oscillating LC circuit consists of a 61.5 mH inductor and a 3.77 μF capacitor. If the maximum charge on the capacitor is 3.56 μC, what are (a) the total energy in the circuit and (b) the maximum current?

Answer 1

`1.68085* 10^(-6)\ J`

0.00739 A

Step-by-step explanation:

Q = Maximum charge on the capacitor =
`3.56\ \mu C`

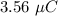
C = Inductor capacitance =
`3.77\ \mu F`

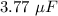
L = Inductance = 61.5 mH

I = Current

Maximum energy in capacitor is given by

`E=(Q^2)/(2C)\\\Rightarrow E=((3.56* 10^(-6))^2)/(2* 3.77* 10^(-6))\\\Rightarrow E=1.68085* 10^(-6)\ J`

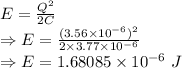
Total energy in the circuit is
`1.68085* 10^(-6)\ J`

Energy is also given by

`E=(LI^2)/(2)\\\Rightarrow I=\sqrt{(2E)/(L)}\\\Rightarrow I=\sqrt{(2* 1.68085* 10^(-6))/(61.5* 10^(-3))}\\\Rightarrow I=0.00739\ A`

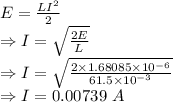
The maximum current in the circuit is 0.00739 A