Question

Your local pizza chain claims that the delivery time of their pizzas is normally distributed with a mean of 30 minutes and standard deviation of 10 minutes. Twenty of your friends in different locations order pizzas and the average delivery time is 42 minutes with standard deviation of 10 minutes. Compute a one-sample t statistic. Do you have a reason to disbelieve the chain’s claim?

Answer 1

Using a significance level of 5% you can reject the null hypothesis, this means that the average time it takes to make a delivery from the local pizza chain isn't what the chain claims.

Explanation:

Hello!

Your study variable is X: time that takes to make a delivery from the local pizza chain.

X~N(μ; σ²)

μ= 30 min

σ= 10 min

The hypothesis is:

H₀: μ = 30

H₁: μ ≠ 30

α: 0,05

(There is no level of significance so I've choose one of the most common)

t= X[bar] - μ ~t
`_(n-1)`

S/√n

The rejection region is two-tailed, the critical number are:

`t_(n-1;\alpha/2) = t_(19;0.025) = -2.093`

`t_(n-1;1-\alpha /2) = t_(19; 0.975)  =2.093`

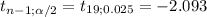
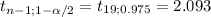
Sample:

n= 20

X[bar]= 42

S= 10

t= X[bar] - μ = 42 - 30 = 5.37

S/√n 10/√20

Using a significance level of 5% you can reject the null hypothesis, this means that the average time it takes to make a delivery from the local pizza chain isn't what the chain claims.

I hope it helps!