Answer: From graph,
inequality 1: y >
 x+(-2)
x+(-2)
inequality 2: y > (-4)x+2
Explanation:
The graph shows two lines on the X-Y plane.
Step 1: Find the equation of a line.
From figure, One line is passing through (3,0) and (0,-2)
Slope of line is given by m=
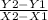
m=
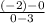
m=

Y-intercept isc=(-2)
The equation of line is given by y=mx+c
Therefore, y=
 x+(-2)
x+(-2)
From figure, Another line is passing through (0.5,0) and (0,2)
Slope of line is given by m=
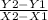
m=

m=
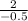
m=(-4)
Y-intercept isc=(2)
The equation of line is given by y=mx+c
Therefore, y=(-4)x+2
Step 2: Test of origin and finding inequality
For y=
 x+(-2)
x+(-2)
Let suppose, y >
 x+(-2)
x+(-2)
This line is shaded toward the origin then, inequality must satisfy the origin
Test for origin says,
0 >
 (0)+(-2)
(0)+(-2)
0 > (-2)
TRUE.
y >
 x+(-2) is required inequality
x+(-2) is required inequality
For y=(-4)x+2
Let suppose, y > (-4)x+2
This line is shaded away from the origin then, inequality must not satisfy the origin
Test for origin says,
0 >
 (0)+(-2)
(0)+(-2)
0 > (+2)
FALSE, so that y > (-4)x+2 does not satisfy the origin
y > (-4)x+2 is required inequality
Thus,
inequality 1: y >
 x+(-2)
x+(-2)
inequality 2: y > (-4)x+2