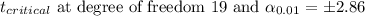Answer:
99% Confidence interval: (183,246)
Explanation:
We are given the following data set:
141, 144, 150, 161, 169, 179, 186, 194, 199, 209, 219, 220, 226, 237, 254, 261, 275, 278, 286, 295
Formula:

where
 are data points,
are data points,
 is the mean and n is the number of observations.
is the mean and n is the number of observations.
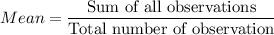
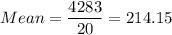
Sum of squares of differences = 45922.55
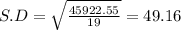
99% Confidence interval:
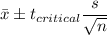
Putting the values, we get,