Question

Consider a motor that exerts a constant torque of 25.0 nâ‹…m to a horizontal platform whose moment of inertia is 50.0 kgâ‹…m2. Assume that the platform is initially at rest and the torque is applied for 12.0 rotations. Neglect friction.

Answer 1

W = 1884J

Step-by-step explanation:

This question is incomplete. The original question was:

Consider a motor that exerts a constant torque of 25.0 N.m to a horizontal platform whose moment of inertia is 50.0kg.m^2 . Assume that the platform is initially at rest and the torque is applied for 12.0rotations . Neglect friction.

How much work W does the motor do on the platform during this process? Enter your answer in joules to four significant figures.

The amount of work done by the motor is given by:

`W=\Delta K`

`W= 1/2*I*\omega f^2-1/2*I*\omega o^2`

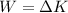
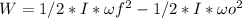
Where I = 50kg.m^2 and ωo = rad/s. We need to calculate ωf.

By using kinematics:

`\omega f^2=\omega o^2+2*\alpha*\theta`

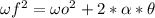
But we don't have the acceleration yet. So, we have to calculate it by making a sum of torque:

`\tau=I*\alpha`

`\alpha=\tau/I` =>
`\alpha = 0.5rad/s^2`

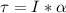
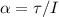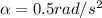
Now we can calculate the final velocity:

`\omega f = 8.68rad/s`

Finally, we calculate the total work:

`W= 1/2*I*\omega f^2 = 1883.56J`

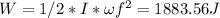
Since the question asked to "Enter your answer in joules to four significant figures.":

W = 1884J