Question

A rectangle has the length of 22 inches less than 7 times the width. If the area of the rectangle is 3197 square inches, find the length of the rectangle

Answer 1

The length of rectangle is 139 inches

Solution:

Given that, area of the rectangle is 3197 square inches

Let "L" be the length of rectangle and "W" be the width of rectangle

Also given that rectangle has the length of 22 inches less than 7 times the width

Length = 7 times width - 22

L = 7W - 22

The area of rectangle is given as:

`\text {Area of rectangle }=\text { length } * \text { width }`

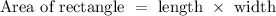
Substituting the values we get,

`\begin{array}{l}{3197=(7 W-22)(W)} \\\\ {3197=7 W^(2)-22 W} \\\\ {7 W^(2)-22 W-3197=0}\end{array}`

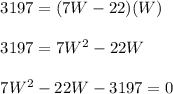
On solving the above quadratic equation using quadratic formula,

`\text {For the quadratic equation } a x^(2)+b x+c=0 \text { where } a \\eq 0`

`x=\frac{-b \pm \sqrt{\left(b^(2)-4 a c\right)}}{2 a}`

`\begin{array}{l}{\text {Here in } 7 \mathrm{W}^(2)-22 \mathrm{W}-3197=0} \\\\ {a=7 ; b=-22 ; c=-3197}\end{array}`

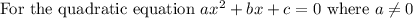
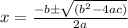
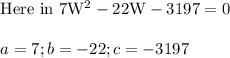
Substituting in above quadratic formula,

`\begin{array}{l}{W=\frac{-(-22) \pm \sqrt{\left((-22)^(2)-4(7)(-3197)\right)}}{2 * 7}} \\\\ {W=(22 \pm √(90000))/(14)=(22 \pm 300)/(14)} \\\\ {W=(22+300)/(14) \text { or } W=(22-300)/(14)} \\\\ {W=23 \text { or } W=-19.85}\end{array}`

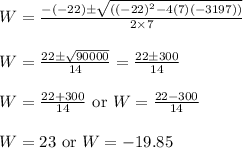
Since width of rectangle cannot be negative, ignore negative value of "W"

So width W = 23 inches

Length L = 7W - 22 = 7(23) - 22 = 139 inches

Thus length of rectangle is 139 inches