Question

A student believes that no more than 20% (i.e., (less than or equal to) 20%) of the students who finish a statistics course get an A. A random sample of 100 students was taken. Twenty-four percent of the students in the sample received A's.

a. State the null and alternative hypotheses.
b. Using the critical value approach, test the hypotheses at the 1% level of significance.
c. Using the p-value approach, test the hypotheses at the 1% level of significance.
Below are the answers. I need help on how these are found with any and all proofs/formulas please!!
a. H0: P (less than or equal to) 0.2
Ha: P > 0.2
b. Do not reject H0; test statistic Z = 1 < 2.33
c. Do not reject H0; p-value = 0.1587 > 0.01

Answer 1

a. The proportion of students who finish a statistics course and get an A is greater than 20%. b. In this case, the test statistic is 1, which is less than the critical value of 2.33. Therefore, we do not reject the null hypothesis. c. In this case, the p-value is 0.1587, which is greater than the significance level of 0.01. Therefore, we do not reject the null hypothesis.

Step-by-step explanation:

The questions can be answered as -

a. Null hypothesis (H0): The proportion of students who finish a statistics course and get an A is less than or equal to 20%. Alternative hypothesis (Ha): The proportion of students who finish a statistics course and get an A is greater than 20%.

b. To test the hypotheses using the critical value approach at the 1% level of significance, we compare the test statistic Z with the critical value. If the test statistic is greater than the critical value, we reject the null hypothesis. In this case, the test statistic Z is 1, which is less than the critical value of 2.33. Therefore, we do not reject the null hypothesis.

c. To test the hypotheses using the p-value approach at the 1% level of significance, we compare the p-value with the significance level. If the p-value is less than the significance level, we reject the null hypothesis. In this case, the p-value is 0.1587, which is greater than the significance level of 0.01. Therefore, we do not reject the null hypothesis.

Answer 2

Step-by-step explanation:

Hello!

Your study variable is

X: Number of students that finished tha statistics course with an a, in a sample of 100 students.

This variable has a binomial distribution X~Bi(n;ρ)

The student believes that no more than 20% of the students pass the course with an A. This percentage is the population proportion symbolically: ρ ≤ 0.20, and is your null hypothesis., so:

a.

H₀: ρ ≤ 0.20

H₁: ρ > 0.20

α: 0,01

The statistic to use is the Z approximation for the proportions. To assemble this statistic, the central limit theorem is applied, this theorem allows us, at a sufficiently large sample size (n≥30), to approximate the distribution of the sample proportion (^p) to normal:

^p ≈ N(p; p(1-p)(1/n))

The statistic formula is:

Z= ^p - p ≈ N(0;1)

√p(1-p)(1/n)

the sample proportion is ^p= 0.24

b.

Z= 0.24 - 0.2 = 1

√0.2*0.8(1/100)

The rejection region of this hypothesis is one-tailed (positive) If you ever have trouble identifying the type of rejection region look at the direction of the alternative hypothesis, if it has the symbol < then is a one-tailed, to the left, rejection region. If it has the symbol > then is a one-tailed, to the right, rejection region and if it has the ≠ symbol, it means the rejection region is "split" in two, i.e. two-tailed.

The critical value is:

`Z_(1-\alpha ) = Z_(0.99) = 2.33`

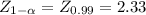
If Z ≥ 2.33, then you reject the null hypothesis.

If Z < 2.33, then you do not reject the null hypothesis.

The decision is to not reject the null hypothesis.

c.

The p-value is defined as the probability corresponding to the calculated statistic if possible under the null hypothesis (i.e. the probability of obtaining a value as extreme as the value of the statistic under the null hypothesis).

Symbolically:

P(Z ≥ 1) = 1 - P(Z < 1) = 1 - 0.84134 = 0.15866

You have to look at what is the probability of the calculated Z value, the direction of the p-value is always the same as the rejection region. In this case, is a one-tailed p-value (to the right)

Using the p-value approach, the decision rule is always the same:

If p-value ≤ α, then you reject the null hypothesis.

If p-value > α, then you don't reject the null hypothesis.

Since the p-value 0.15866 > 0.01, then you do not reject the null hypothesis.

As expected, using the two methods you reached the same decision. If not then you have to check your maths.

I hope it helped!